Knot-Particle Associations
With occasionally technical details, part 1/2
So I’ve already offered a soft philosophical walk toward reconsideration of knots as particles. More specific technical observations are worth getting into, with the objective of justifying a ‘diceotope approach’ which needs more discussion to be truly accessible and accurate beyond first order charge accounting.
It’s kind of hard to have a coherent nuclear model without a reasonably good understanding the nucleons inside of said nuclei (the phoneme ‘nuc’ is wearing thin), and so getting to those topologies is the goal. Any attempt to understand the ‘Segre Chart’ data will constantly encounter the wall of uncertainty around internal structural details inside the atom, and it is with that objective in mind that I found myself revisiting ‘archaic’ concepts like a grave thief: the knot theories of Kelvin and Tait, Parson’s Toroidal rings, revisiting Maxwell and MacCullagh; as well as the insights of the more recently deceased and often more obscure: John G Williamson, Norman Cook, Ray Fleming, Alexander G Kyriakos, Yuri Vasilievich Burtaev, and many more folks with some focus on isotopes/nuclei and/or subatomic models and ether representations. There are many comments in the literature which suggest knots as mathematically sound topological defects, propagating through some mechanism which is not specified here in detail.
Unknot as photon topology
The unknot (0_1) is the simplest prime knot topology, with no writhe or self-crossings and is typically considered a sort of degenerate case in knot theory land.
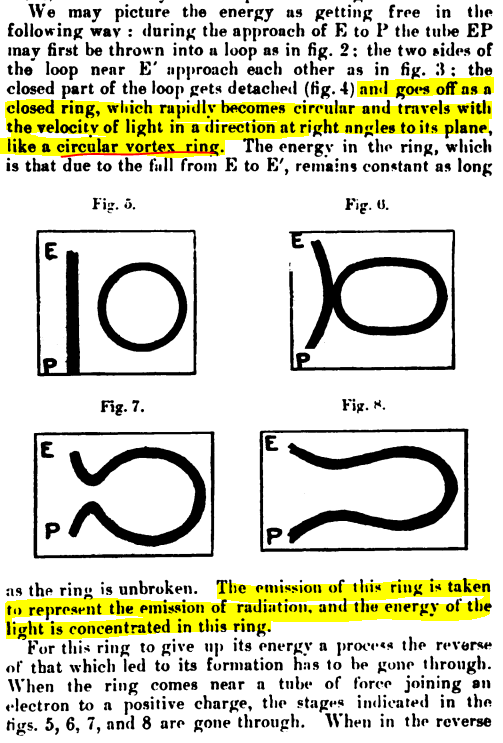
Nonetheless, it can be observed as a vortex-related phenomena in smoke rings, bubble rings, superconductors, insert additional examples here) and if Kelvin's vortex knot concept is taken at face value, the simplest knot and the most common ‘wavicle’ should have a lot in common.
This association was noted explicitly by J.J. Thomson seemingly in the electric potential itself and had seemingly a very clear vision for the nature of the photon in 1925 (turned onto this by A.G. Kyriakos):
The commonly shown infinite sinusoidal wave-train model is good for describing groups of photons, but doesn't make sense for individual photons, and might be a remnant of ‘rays’ in traditional optics rather than a modern post-quantum conceptualization. (You will see people try to split the difference here with wave packet visualizations and the like)
While our description of photon polarization is rather well captured for groups/beams of photons in Stokes vectors and Mueller matrices, with linear and circular polarizations accounted for if not explicitly described, we rarely try to ask what these polarization states imply about a single photon without resorting to the plane wave model, and each photon acts as a transient contribution to some part of the stokes vector. (Spectroscopic ellipsometry makes great use of these methods)
It seems likely that the energy of photons can be accommodated by some sinusoidal or helical path around the ring which satisfies a sort debroglie condition in addition to whatever other constraints are needed, but the relationship between wavelength and ‘photon size’ remains inverted in that higher energies imply smaller structures, more relevant as the topology becomes more knotted. J.J. Thompson suggests that the size is tied directly to the wavelength as a circumference - this seems not unreasonable.
Accounting for polarization raises a few possible options, and questions about the propagation behavior remain. If J.J Thompson’s view is taken, it seems that photons might propagate ‘edge on’ like a frisbee within the plane of the ring, rather unlike a smoke ring, which travels normal to the plane of the ring while poloidally rotating. In this case, perhaps the electric oscillation of each photon would be within the plane of the ring itself (or normal to it as Thompson suggests in his 1925 paper), and the cases of linear, circular, and elliptical polarization relate back to the relative rotation of the ring as it travels like a frisbee.
Alternatively, one could imagine some mapping to this topology where the orientation of the ring with respect to its direction of travel provides the definition for polarization, with more ‘smoke ring like’ propagation associating with the circular states, and frisbee-like propagation associating with the linear states. (A suspicion: More minds on this problem would likely quickly rule out or favor one interpretation over another with deductive reasoning and specific details.)
The spin of the unknot topology without enforcing additional details is not obvious (to me anyway), beyond not appearing fractional. So, 1?
The ‘speed of light’ as traditionally defined would be interpreted as the traveling speed of the total topology, while the underlying ‘pilot wave’ (or whatever) would seemingly need to be as fast or locally faster, for the total structure to ‘keep up’.
Link as Neutrino topology
This association is more tentative but seems to follow from the above. A pair of linked unknot topologies (like a Hopf link), traveling together in some direction, would carry more momentum than a single photon, while still possessing no writhe/charge. Some hesitation towards self-interaction is assumed, so that the identity can be maintained barring further collisions with other knot topologies. The relevance of these little buggers arises in the context of muon decay, neutron decay, and isotope stability, but otherwise it’s not clear they are doing much else. In this context, ‘entanglement’ has a literal and direct interpretation, unrelated to modern conceptions of ‘quantum entanglement’, and it is specific to neutrinos and muons (and likely other unstable zoo particles)
Given the implied interpretation of beta decay, see below, it might be possible that TWO neutrinos are actually released rather than one (would we notice? We almost didn’t notice them in the first place!).
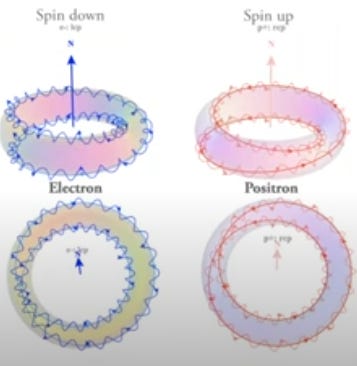
‘Mobius’ as electron topology
(photo pilfered from Arnie Benn’s talk linked below)
This particular (mobius) association requires some explanation, as there is no prime knot traditionally located between the unknot and the trefoil knot in the table of prime knots developed using Reidemeister 1, and this association likely seems a non-sequitur on this basis to those with some background. I swear, this isn’t heresy. Knot theorists have largely been focused on things like classifying knots with n>? crossings, and so a little anomaly between the unknot and the trefoil has gone unnoticed. In the spirit of some other topology proofs I offer you this:
A belt with a half twist in it is distinct from a ‘normal’ belt (as anyone who has worn it twisted by accident can attest), and this might be called 1_1 in prime knot terminology. This difference is not well considered by mathematical ‘knot theory’ (though topologists love their mobiuses), and so it is not typically considered a ‘proper knot’ to this point. Its recognition perhaps complicates the proposed descriptions of knots and links and mathematicians will probably want to address this in detail, but becomes more clear in the context of ribbons:
When writhe is introduced (in a quantized way?) into an otherwise ‘unknotted’ topology, the resulting structure has a low-energy state in which it folds onto itself in a double loop (as well as it can, there is always a single crossover in projection). The choice of twist direction applied to the ‘belt which is not a belt’ yields either left or right handed versions, of equal and opposite writhe, but with a similar degree of ‘tangledness’. This mirror image provides a mechanism for the distinction between matter and antimatter using local topology. The asymmetry of observed handedness is akin to snail shells - every now and again you’ll find one with the opposite handedness but there tends to be a bias. (More to be said here regarding the neutron and handedness of beta decay)
This sort of idea has been proposed by a number of authors, though it’s not well recognized as related to Kelvin’s proposal. Perhaps the best formed model representing this can be found in what I call the ‘Quicycle’ electron, evolving from the proposed model of Williamson and van der Mark. It is worth noting that Williamson was fairly adamant that there was no mobius-ness to this model, but the Siefert surface of this type of ‘double loop’ structure is exactly a mobius strip (see above) - the path defined is the edge of a kind of mobius. Given the spin ½ nature of the electron, it seems notable that a similar behavior is observed in a mobius strip.
He and Arnie Benn further developed this model after van der Mark’s death - it and associated ideas are hosted by the ‘Quicycle Society’, now inherited by Arnie. They attempt to use this model to explain the para-ortho positronium lifetime differences and while some details seem wrong (their explanation for antimatter), the overall approach deserves consideration. Helicity of the ‘pilot wave’ is used to explain antimatter - as stated above, this mechanism seems untrustworthy and ignores the larger topological milieu of the knot insight, as they do not address the handedness they have chosen. The topological explanation for matter/antimatter as mirror images appears preferable, as no specific character of the pilot wave need be invoked to explain observations (yet). Williamson’s electron is interesting because by incorporation of maxwell’s equations (slightly modified, iirc) his double loop/mobius offers a mechanism for the generation of charge from the topological structure.
‘Hu’s Hubius helix’ describes a similar model of a doubly-looped path. Instead of a photon trapped on said path, Hu suggests a massless particle which moves at light speed, which sounds a lot like the same sort of thing. Not terribly insightful but worth noting.
More recently, Brandon Findlay published a paper exploring this model with a fairly simple essentially classical/undergrad approach. It is notable in that he also makes the proton-trefoil association below.
On the more fringe side, there is this website, which is adamant, if not convincing. It’s a sentiment in the zeitgeist.
The Zitter institute deserves notable mention for hosting a variety of ideas around ‘extended electron models’ which include a number of those described above. A summary of these types of models was released in February 2025 which makes some relevant observations.
Notice (visualize?) that this particular topology maps well to a torus, and a poloidal rotation will cause the crossing point (loosely defined) to rotate or spin, to an external observer. Whether or not the pilot wave is bound by light speed (as noted above), this ‘chasing of its own tail’ which occurs by this poloidal rotation may give some mechanism to address previously paradoxical electron properties (Zitterbewegung?) including spin.
It is not clear what ‘detecting’ an extended electron means (scattering from the entire object as opposed to the crossing region?), and no specific scaling estimates have been applied here, but the classical estimates have some relevance. In the context of orbital theory, the idea of the entire electron ‘filling the orbital’ may be more literal than historically intended. Perhaps this double looped path may account for the behavior of transition from lower to higher energy states following photon absorption (leaning on J.J Thompson’s intuition), with a similar shift of the looped path upon emission, suggesting something between the Bohr model and the spherical harmonic/orbital picture using an extended electron.
While this is speculative, it hopefully illustrates that there is some potentially fertile ground for fruitful approaches to grow in, which people are already somewhat aware of - even if only as a shadowy representation in the collective mind.
The Muons & Pions
There is no simple name for the implied muon topology, but if you imagine a photon loop linked around the pseudo-mobius electron described above (there is more than one way to imagine this, possibly accounting for the tau - though that’s a low priority target). This mechanism would create additional self-interference than a typical electron would possess, but it would have the same writhe/charge. The decay mechanism for this then can be visualized as part of the electron’s ‘filament’ being pinched off into one of the unknots of the emitted neutrino link (much as would happen in transitioning between bound states as described above). While orthodox physics is fairly adamant that there are three flavors of neutrino - I’m somewhat skeptical of our assertions about it. We know there’s another neutral momentum carrier of some variety. Beyond that I think some healthy deep dives and arm wrestling will be required to find out what NEEDs to be addressed with certainty.
A model for the Pion using this approach is not so clear, but the difference between charged and uncharged pions is a key element, as their decay modes and half lives are very different, and there is a very subtle mass difference. As the neutral pion decays in a manner akin to positron annihilation, a composition including a single twist of each handedness seems required. The fast decay (8.5×10−17 s) suggests a ‘quasi-degenerate’ topology in that identity is fleeting and unstable (i.e. something mathematicians would consider topologically trivial or ‘goofy’, but potentially still a temporarily identifiable configuration). Ray Fleming suggests the neutral pion is a relativistic positronium (e- + e+), which might give perhaps a better insight into some ‘resonances’ generally if these possibilities are kept in mind (perhaps some are ‘more real’ than others, it’s largely unexplored by anyone with any skeptical eye).
Similar reasoning holds for the charged pions (with 1/100 the lifetime of a muon), excepting that perhaps ‘units’ of writhe may be involved instead, as it is carried through its decay. Neutrino-like linking could also be involved, further complicating the available possibilities.
This leads to a larger point: no further zoo particles are considered herein, but guidelines for that process could be proposed from this approach, made more trustworthy/complete by a dynamic model. As ephemera are of minimal practical importance it is left to someone else to chase, provided that the conceptual groundwork is soundly established (I would talk people out of bothering at this point). Prime knots larger than 4_1 may be good candidates for some longer lived particles with more mass than the neutron, though if the muon model has utility, knots with simple linked photons would also be expected.
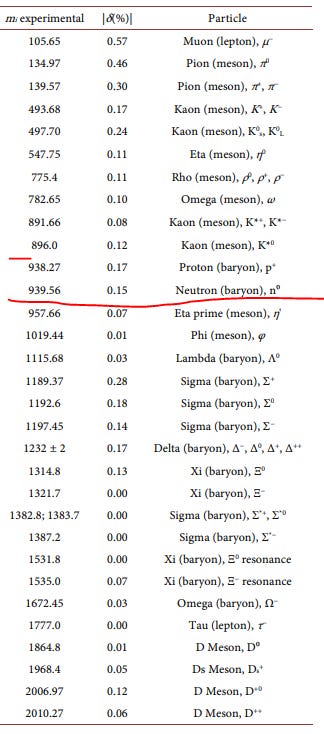
A Particle zoo table from reference here, to give you some idea of what needs at least a minimal explanation:
Given that the neutron is unstable in free space, but stable within a nuclear setting, one must wonder if more complex knot topologies might also find some stability within a nuclear environment, however their symmetries and properties are more complex than the simpler topologies described.
The relationship between 5_1 and 5_2 and heavier unstable zoo particles remains unclear. Would they have a similar mass due to similar complexity, or would the difference in topology produce some jump in mass? It is possible that neither would be stable even within a nuclear environment and so this possibility should be viewed with some suspicion unless evidence arises to vindicate it as a useful phenomena.
Subsack (yeah I said it) is saying that this almost too long to email. For the two of you here reading, tune in next post for specifics about protons and neutrons (the good stuff). I suppose this is sort of just extraneous detail for the nerdiest of physics nerds…